문제 설명 및 제한사항
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
N x M 크기의 행렬 모양의 게임 맵이 있습니다. 이 맵에는 내구도를 가진 건물이 각 칸마다 하나씩 있습니다. 적은 이 건물들을 공격하여 파괴하려고 합니다. 건물은 적의 공격을 받으면 내구도가 감소하고 내구도가 0이하가 되면 파괴됩니다. 반대로, 아군은 회복 스킬을 사용하여 건물들의 내구도를 높이려고 합니다.
적의 공격과 아군의 회복 스킬은 항상 직사각형 모양입니다.
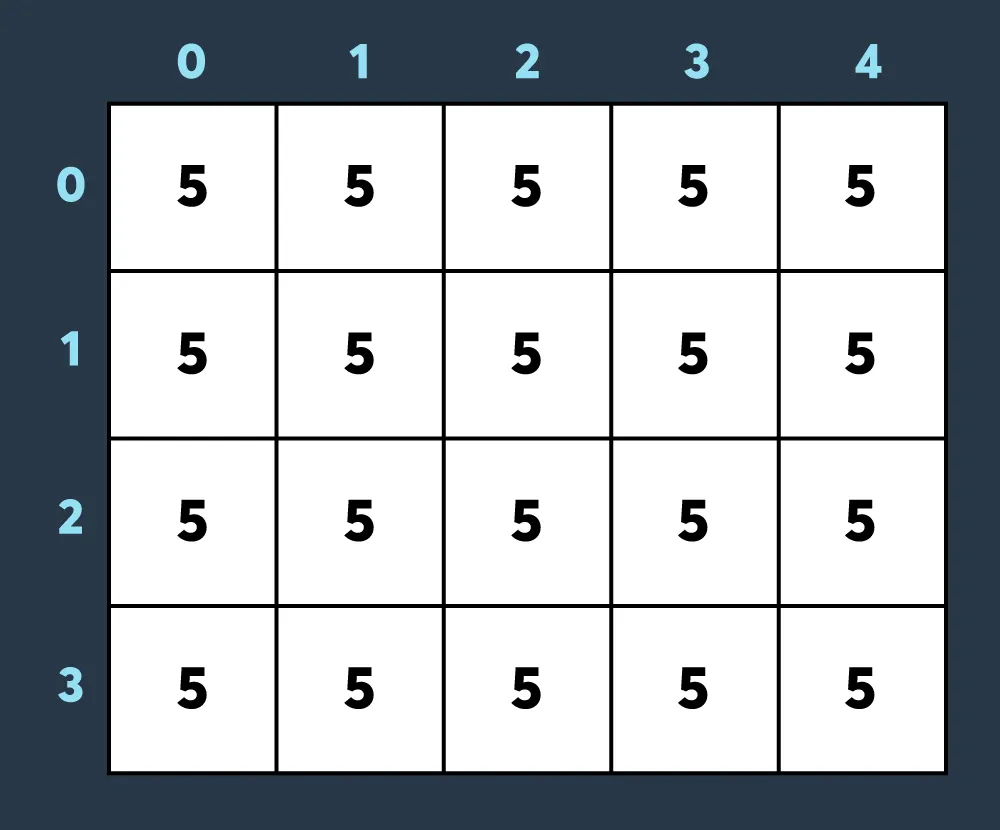
예를 들어, 아래 사진은 크기가 4 x 5인 맵에 내구도가 5인 건물들이 있는 상태입니다.
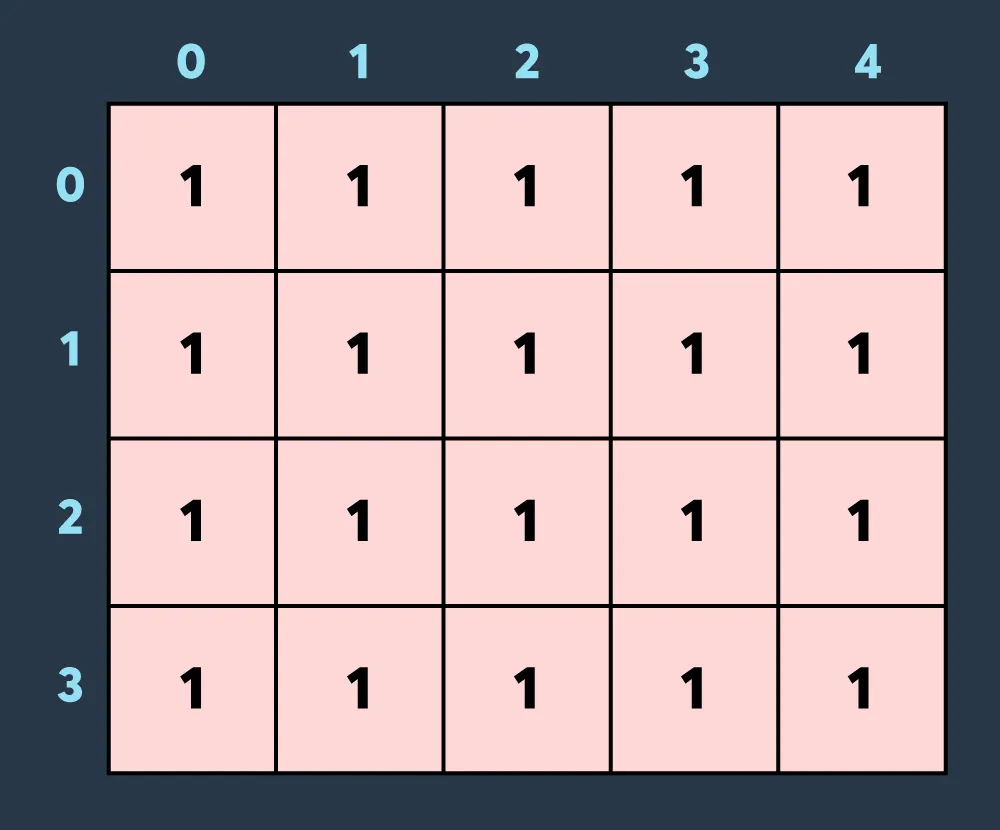
첫 번째로 적이 맵의 (0,0)부터 (3,4)까지 공격하여 4만큼 건물의 내구도를 낮추면 아래와 같은 상태가 됩니다.
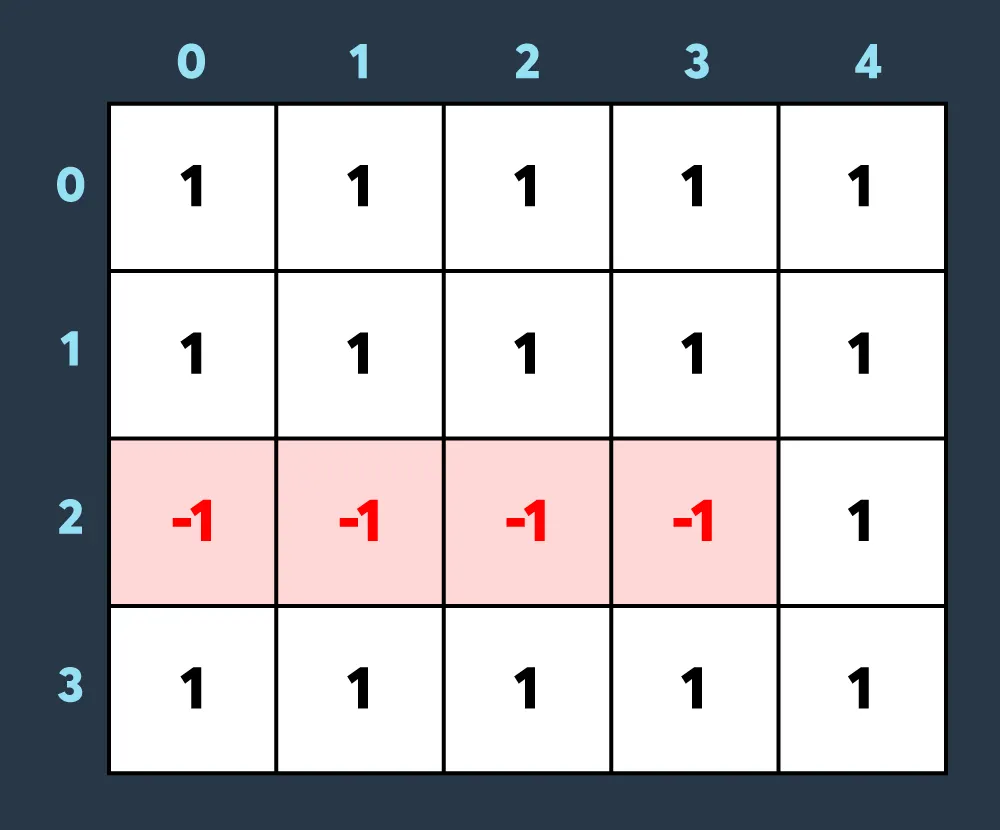
두 번째로 적이 맵의 (2,0)부터 (2,3)까지 공격하여 2만큼 건물의 내구도를 낮추면 아래와 같이 4개의 건물이 파괴되는 상태가 됩니다.
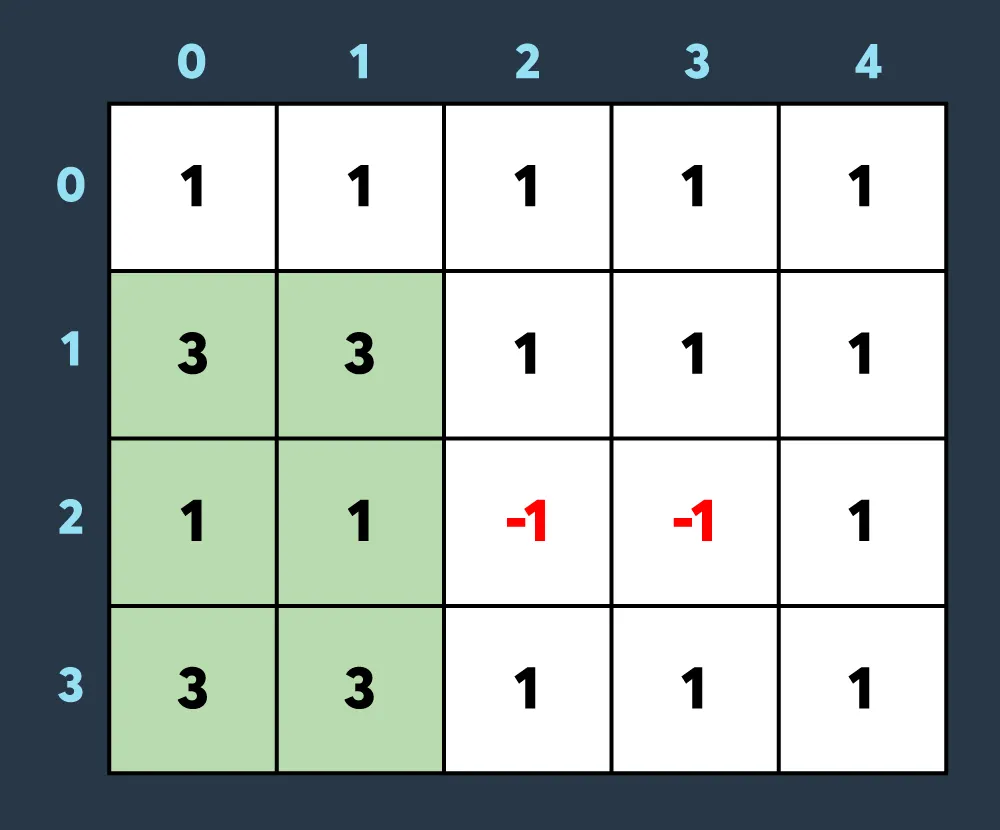
세 번째로 아군이 맵의 (1,0)부터 (3,1)까지 회복하여 2만큼 건물의 내구도를 높이면 아래와 같이 2개의 건물이 파괴되었다가 복구되고 2개의 건물만 파괴되어있는 상태가 됩니다.
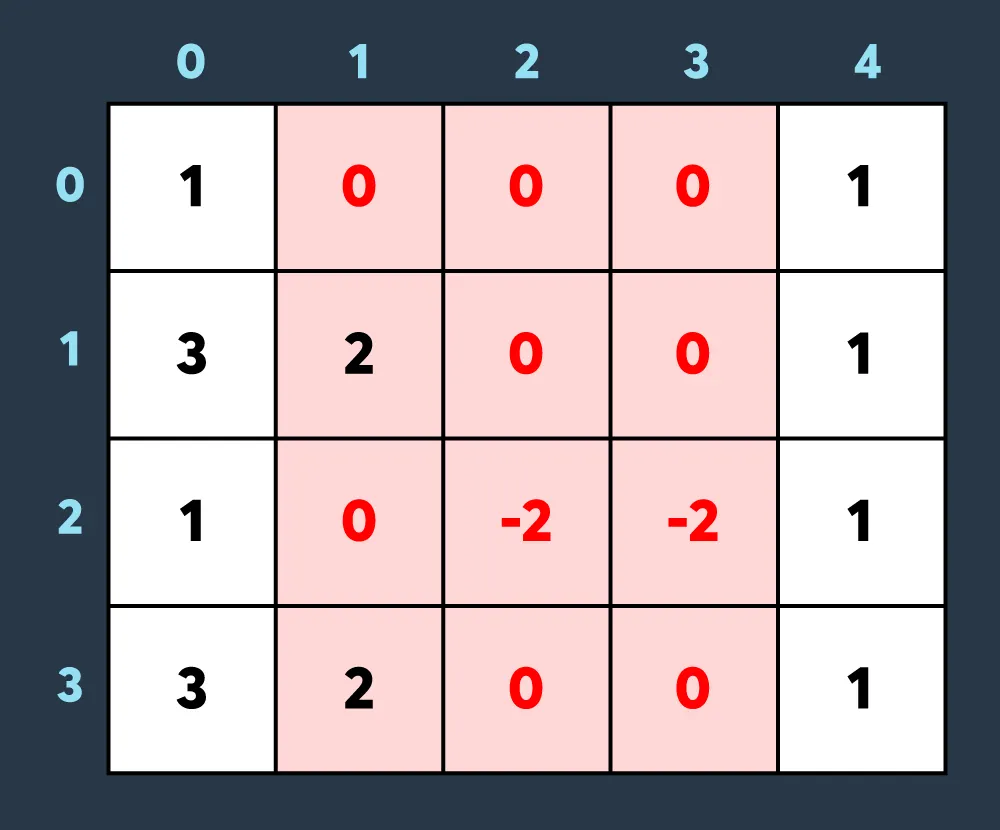
마지막으로 적이 맵의 (0,1)부터 (3,3)까지 공격하여 1만큼 건물의 내구도를 낮추면 아래와 같이 8개의 건물이 더 파괴되어 총 10개의 건물이 파괴된 상태가 됩니다. (내구도가 0 이하가 된 이미 파괴된 건물도, 공격을 받으면 계속해서 내구도가 하락하는 것에 유의해주세요.)
최종적으로 총 10개의 건물이 파괴되지 않았습니다.
건물의 내구도를 나타내는 2차원 정수 배열 board와 적의 공격 혹은 아군의 회복 스킬을 나타내는 2차원 정수 배열 skill이 매개변수로 주어집니다. 적의 공격 혹은 아군의 회복 스킬이 모두 끝난 뒤 파괴되지 않은 건물의 개수를 return하는 solution함수를 완성해 주세요.
제한사항
•
1 ≤ board의 행의 길이 (= N) ≤ 1,000
•
1 ≤ board의 열의 길이 (= M) ≤ 1,000
•
1 ≤ board의 원소 (각 건물의 내구도) ≤ 1,000
•
1 ≤ skill의 행의 길이 ≤ 250,000
•
skill의 열의 길이 = 6
•
skill의 각 행은 [type, r1, c1, r2, c2, degree]형태를 가지고 있습니다.
◦
type은 1 혹은 2입니다.
▪
type이 1일 경우는 적의 공격을 의미합니다. 건물의 내구도를 낮춥니다.
▪
type이 2일 경우는 아군의 회복 스킬을 의미합니다. 건물의 내구도를 높입니다.
◦
(r1, c1)부터 (r2, c2)까지 직사각형 모양의 범위 안에 있는 건물의 내구도를 degree 만큼 낮추거나 높인다는 뜻입니다.
▪
0 ≤ r1 ≤ r2 < board의 행의 길이
▪
0 ≤ c1 ≤ c2 < board의 열의 길이
▪
1 ≤ degree ≤ 500
▪
type이 1이면 degree만큼 건물의 내구도를 낮춥니다.
▪
type이 2이면 degree만큼 건물의 내구도를 높입니다.
•
건물은 파괴되었다가 회복 스킬을 받아 내구도가 1이상이 되면 파괴되지 않은 상태가 됩니다. 즉, 최종적으로 건물의 내구도가 1이상이면 파괴되지 않은 건물입니다.
정확성 테스트 케이스 제한 사항
•
1 ≤ board의 행의 길이 (= N) ≤ 100
•
1 ≤ board의 열의 길이 (= M) ≤ 100
•
1 ≤ board의 원소 (각 건물의 내구도) ≤ 100
•
1 ≤ skill의 행의 길이 ≤ 100
◦
1 ≤ degree ≤ 100
효율성 테스트 케이스 제한 사항
•
주어진 조건 외 추가 제한사항 없습니다.
아이디어 및 해결 방법
프로그래머스 레벨 3 ‘파괴되지 않은 건물’ 문제는 2차원 배열 내의 특정 범위에 일정한 숫자를 더하거나 빼는 연산을 반복하여 최종적으로 건물의 내구도가 1 이상인 배열의 원소의 수를 구하는 문제입니다.
가장 단순한 풀이를 떠올려 보면, 갱신이 일어나는 직사각형 내의 원소들을 순회하면서, degree만큼 더해주거나 빼주는 것을 반복하는 방식으로 해결이 가능합니다. 하지만 당연히 이 방법으로는 효율성 테스트를 통과하지 못합니다. 최악의 경우 대충 (skill의 최대 개수) x (직사각형의 최대 크기) = (250000) x (1000000) = 2.5 x 10^11번 정도의 연산이 필요하니까요. 갱신 과정을 최대한 간단하게 만드는 것이 중요하겠네요!
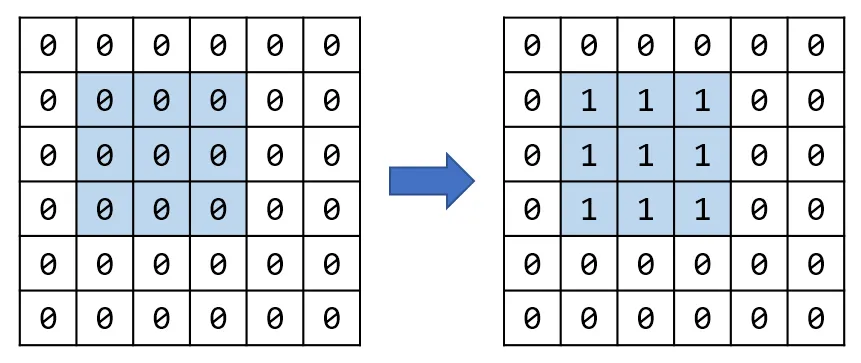
갱신이 항상 직사각형 범위로 일어난다는 점에 착안하면 아이디어를 떠올려볼 수 있습니다. 아래와 같은 6x6 맵에서 색칠된 3x3 영역을 갱신한다고 생각해봅시다.
여기서 아이디어는, 오른쪽 상태와 같이 색칠된 3x3 영역이 1로 바뀐 상태가 어떤 배열의 누적합이라고 생각하는 것입니다.
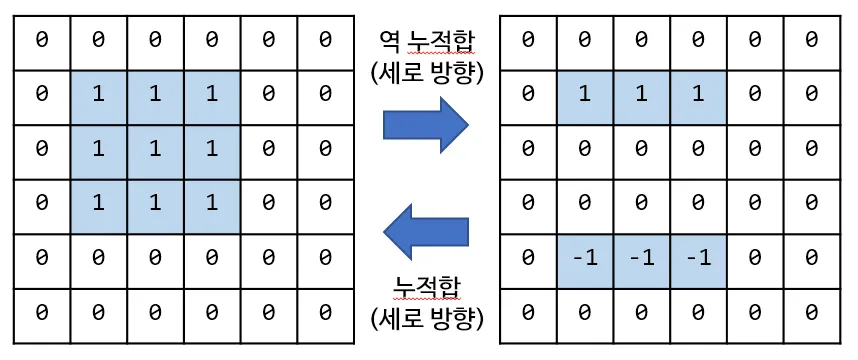
우선 세로 방향만 고려하여 “역 누적합”을 구해보면 아래와 같습니다. 왼쪽과 오른쪽 2차원 배열이 누적합 연산에 의해 정확히 같은 정보를 나타내지만, 오른쪽 배열에 필요한 연산의 수가 더 적음을 알 수 있습니다. 갱신되는 직사각형의 행 개수를 R, 열 개수를 C라 하면
•
왼쪽의 단순한 갱신에 필요한 연산은 개
•
오른쪽의 역 누적합 배열 상의 갱신에 필요한 연산은 개
따라서 대략 배 만큼 연산 횟수를 줄일 수 있게 됐네요!
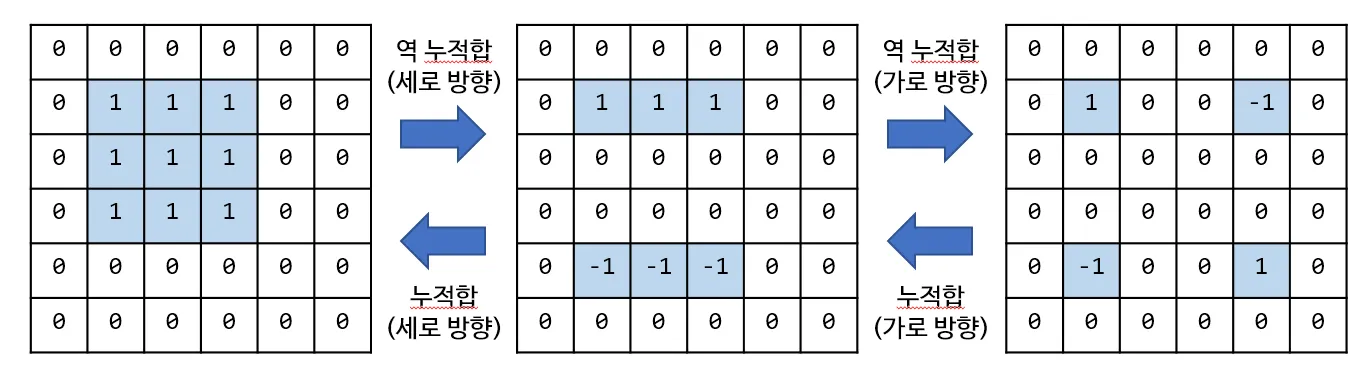
열 방향의 역 누적합 배열에서, 행 방향으로 한번 더 역 누적합 연산을 수행할 수 있을까요?
당연히 가능합니다. 결과적으로 맨 왼쪽의 연산과 동일한 정보를 가지는 연산을 얻어낼 수 있었네요!
이제 이 원리를 응용하면 문제는 쉽게 풀립니다. 모든 갱신은 가장 오른쪽의 (역 누적합)^2 배열 (delta)에서 수행하고, 최종적으로 가로 → 세로 방향의 누적합을 수행하면 최종 상태의 이차원 배열을 얻을 수 있게 됩니다.
참고
역 누적합 배열은 행 방향 혹은 열 방향의 변화량만을 저장한다는 점에서 미분/도함수의 개념으로 기억해 두는 것도 좋을 것입니다.
코드
def solution(board, skill):
# 2차원 세그먼트 트리로 해결해보려 헀으나... 효율성 테스트를 통과하지 못했다
# 다만 약 10만개 정도까지의 쿼리는 처리할 수 있는 것으로 보였다.
# 아쉽지만 누적합 풀이로 해결!
R, C = len(board), len(board[0])
delta = [[0] * (C+1) for _ in range(R+1)]
for op, rmin, cmin, rmax, cmax, degree in skill:
degree = -degree if op == 1 else degree
delta[rmin][cmin] += degree
delta[rmax+1][cmin] -= degree
delta[rmin][cmax+1] -= degree
delta[rmax+1][cmax+1] += degree
for r in range(R):
for c in range(1, C):
delta[r][c] += delta[r][c-1]
for c in range(C):
for r in range(1, R):
delta[r][c] += delta[r-1][c]
return sum(board[r][c] + delta[r][c] > 0 for r in range(R) for c in range(C))
Python
복사
출처
프로그래머스 코딩테스트 연습 https://school.programmers.co.kr/learn/challenges