문제 설명 및 제한사항
문제 설명
길이가 같은 두 개의 큐가 주어집니다. 하나의 큐를 골라 원소를 추출(pop)하고, 추출된 원소를 다른 큐에 집어넣는(insert) 작업을 통해 각 큐의 원소 합이 같도록 만들려고 합니다. 이때 필요한 작업의 최소 횟수를 구하고자 합니다. 한 번의 pop과 한 번의 insert를 합쳐서 작업을 1회 수행한 것으로 간주합니다.
큐는 먼저 집어넣은 원소가 먼저 나오는 구조입니다. 이 문제에서는 큐를 배열로 표현하며, 원소가 배열 앞쪽에 있을수록 먼저 집어넣은 원소임을 의미합니다. 즉, pop을 하면 배열의 첫 번째 원소가 추출되며, insert를 하면 배열의 끝에 원소가 추가됩니다. 예를 들어 큐 [1, 2, 3, 4]가 주어졌을 때, pop을 하면 맨 앞에 있는 원소 1이 추출되어 [2, 3, 4]가 되며, 이어서 5를 insert하면 [2, 3, 4, 5]가 됩니다.
다음은 두 큐를 나타내는 예시입니다.
queue1 = [3, 2, 7, 2]
queue2 = [4, 6, 5, 1]
두 큐에 담긴 모든 원소의 합은 30입니다. 따라서, 각 큐의 합을 15로 만들어야 합니다. 예를 들어, 다음과 같이 2가지 방법이 있습니다.
1.
queue2의 4, 6, 5를 순서대로 추출하여 queue1에 추가한 뒤, queue1의 3, 2, 7, 2를 순서대로 추출하여 queue2에 추가합니다. 그 결과 queue1은 [4, 6, 5], queue2는 [1, 3, 2, 7, 2]가 되며, 각 큐의 원소 합은 15로 같습니다. 이 방법은 작업을 7번 수행합니다.
2.
queue1에서 3을 추출하여 queue2에 추가합니다. 그리고 queue2에서 4를 추출하여 queue1에 추가합니다. 그 결과 queue1은 [2, 7, 2, 4], queue2는 [6, 5, 1, 3]가 되며, 각 큐의 원소 합은 15로 같습니다. 이 방법은 작업을 2번만 수행하며, 이보다 적은 횟수로 목표를 달성할 수 없습니다.
따라서 각 큐의 원소 합을 같게 만들기 위해 필요한 작업의 최소 횟수는 2입니다.
길이가 같은 두 개의 큐를 나타내는 정수 배열 queue1, queue2가 매개변수로 주어집니다. 각 큐의 원소 합을 같게 만들기 위해 필요한 작업의 최소 횟수를 return 하도록 solution 함수를 완성해주세요. 단, 어떤 방법으로도 각 큐의 원소 합을 같게 만들 수 없는 경우, -1을 return 해주세요.
제한사항
•
1 ≤ queue1의 길이 = queue2의 길이 ≤ 300,000
•
1 ≤ queue1의 원소, queue2의 원소 ≤ 10^9
•
주의: 언어에 따라 합 계산 과정 중 산술 오버플로우 발생 가능성이 있으므로 long type 고려가 필요합니다.
아이디어 및 해결 방법
두 단계로 해결합니다.
1.
두 큐의 원소 합을 같게 만들 수 있는지 판단하고,
2.
가능하다면, 필요한 insert/pop 작업의 최소 횟수를 계산합니다.
1.
먼저 두 큐의 원소 합을 같게 만들 수 있는지는 어떻게 판단하면 될까요? 몇 가지 성질을 떠올려 적어 두고 생각해 봅시다.
a.
두 큐에 존재하는 모든 수의 합을 라 하면, 두 큐의 합이 같아진 시점에서 각 큐의 숫자 합은 입니다.
b.
한 큐에서 숫자를 pop하여 다른 큐에 insert하는 연산은, 쉽게 말해서 한 큐의 가장 왼쪽 원소를 제거하여 다른 큐의 가장 오른쪽에 붙여넣는 것입니다.
c.
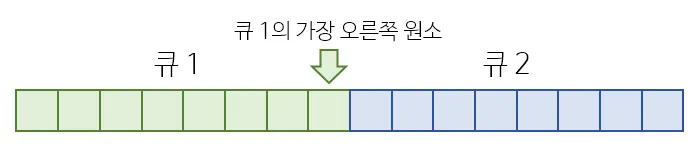
이 때, 아래 그림과 같이 한 큐와 다른 큐를 서로 이어 붙여 하나의 배열로 표현했다고 상상해봅시다. 큐 1의 가장 오른쪽 원소의 index를 나타내는 pointer를 하나 가지고 있으면 좋겠네요.
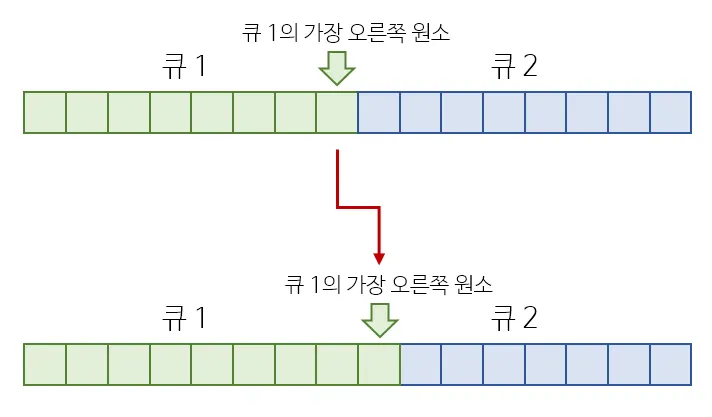
위의 상태에서, 큐 2의 원소 하나를 pop하여 큐 1에 insert하는 연산을 어떻게 나타낼 수 있을까요?
간단합니다! 큐 1의 가장 오른쪽 원소를 나타내는 포인터를 1 증가시키면 됩니다. 두 큐를 하나의 배열로 표현하는 방법이 아직까지는 굉장히 효과적인 것 같네요.
그러면 큐 1의 원소 하나를 pop하여 큐 2에 insert하려면 어떻게 할 수 있을까요? 큐 1의 가장 왼쪽 원소를 제거하고 배열의 가장 끝에 추가하면 되겠지만, 앞선 연산만큼 우아한 방법인 것 같진 않네요. 더 좋은 방법이 있을까요? 큐 1의 왼쪽에 큐 2가 있으면 좋을 것 같은데…
배열 자체를 두번 반복해서 붙여두면 어떨까요?
앞선 큐 1-큐 2 상황과 똑같이, “큐 2의 가장 오른쪽 원소를 나타내는 포인터”를 1 증가시키면 되겠네요!
여기서 알 수 있는 것은, pop/insert 연산은 결국 위의 큐1-큐2-큐1-큐2 배열에서 포인터를 이동시키는 것에 대응되기 때문에, 어떤 큐의 원소의 합이 가 될 수 있는지 판단하는 것은 결국 위 배열에서 합이 가 되는 구간합이 존재하는지 판단하는 것과 같다는 겁니다. 이건 누적합 배열로 쉽게 해결할 수 있겠네요!
2.
최소 연산 횟수는 어떻게 구할 수 있을까요? 우선 위 작업으로 구간합이 인 구간들을 모두 얻었다고 생각해 봅시다 intervals: 구간 (i, j)들의 배열
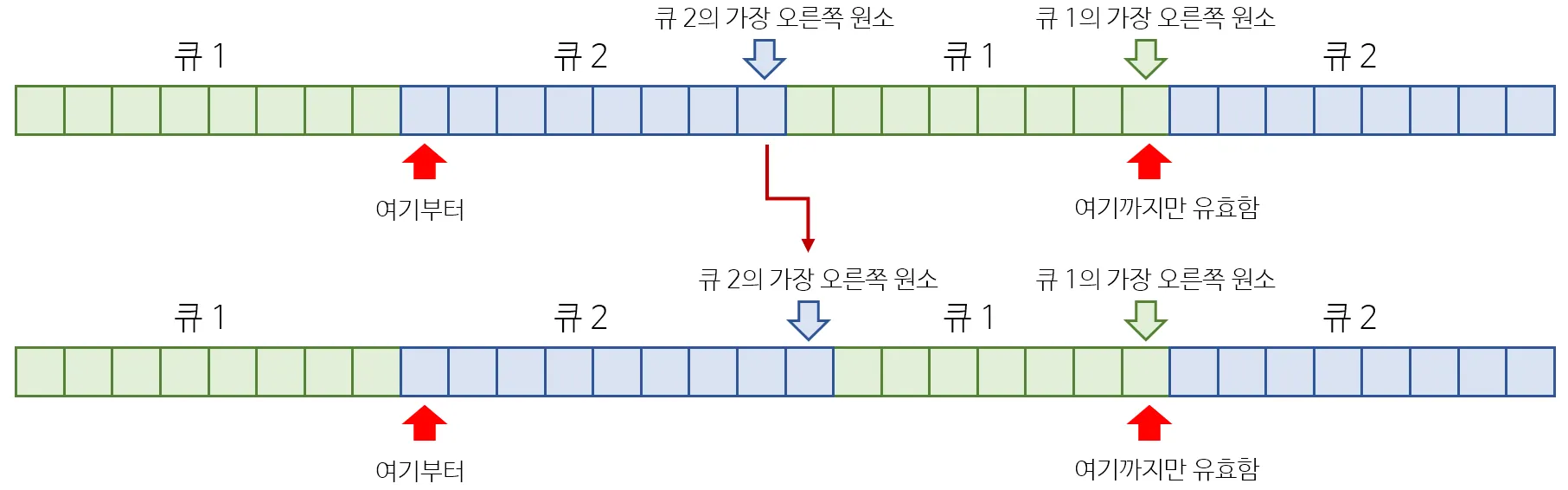
이 때, j가 큐 1의 크기 n1보다 큰 구간 중 i가 가장 작은 구간을 생각해 봅시다. 즉 가장 왼쪽에 있는 구간인 것이죠. (참고로 j가 n1보다 작은 구간은 고려할 필요가 없습니다. insert/pop 연산에 의해서 포인터는 항상 오른쪽 으로 움직이기 때문에, 해당 구간에 딱 맞게 큐 1을 구성할 방법이 없기 때문입니다. 잘 고민해보면 이해가 될 겁니다!)
큐 1이 구간 (i, j)에 딱 맞도록 연산을 수행하는 방법은 위와 같습니다. 큐 1에서 i번 pop하고, 큐 2에서는 j - n1번 pop하면 됩니다. 즉, 정답은 i + (j - n1)이 됩니다.
코드
def solution(queue1, queue2):
# 우선 큐의 원소 합을 같게 할 수 있는지부터 봅시다.
# 큐 원소의 총 개수를 n, 총합을 s라 할 때
# 큐 두개를 합쳐서 두번 반복한 배열에서
# 길이 최대 n-1인 구간합이 s//2가 될 수 있는지를 판단하면 됩니다.
# 누적합 배열, 투 포인터를 활용합니다.
n1, n2 = len(queue1), len(queue2); n = n1 + n2
s = sum(queue1) + sum(queue2)
arr = (queue1 + queue2) * 2
i, j = 0, 0
cumsum = [0]
for x in arr:
cumsum.append(cumsum[-1] + x)
intervals = []
while j < len(arr):
if cumsum[j] - cumsum[i] < s//2:
j += 1
elif cumsum[j] - cumsum[i] > s//2:
i += 1
else: # 합이 s//2인 경우입니다.
if j - i <= n-1:
intervals.append((i, j))
j += 1
# 구간합이 s//2가 되는 경우가 없으면 방법이 없다는 뜻입니다.
if len(intervals) == 0:
return -1
# 이제 어떤 수를 조합하면 합이 s//2가 되는지 그 경우들을 알았으니,
# 그 경우들 중 큐 push/pop 작업을 최소한으로 하는 경우를 세어봅시다.
for i, j in intervals:
if j >= n1:
return i + (j - n1)
Python
복사
출처
프로그래머스 코딩테스트 연습 https://school.programmers.co.kr/learn/challenges