문제 설명 및 제한사항
문제 설명
테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.
•
조각은 한 번에 하나씩 채워 넣습니다.
•
조각을 회전시킬 수 있습니다.
•
조각을 뒤집을 수는 없습니다.
•
게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.
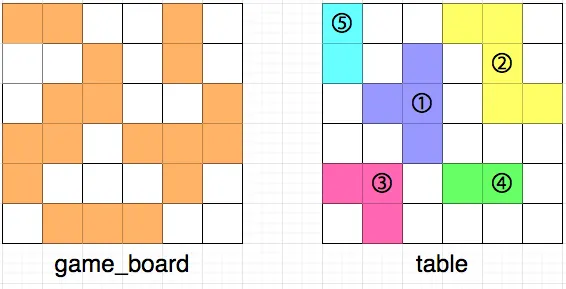
다음은 퍼즐 조각을 채우는 예시입니다.
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.
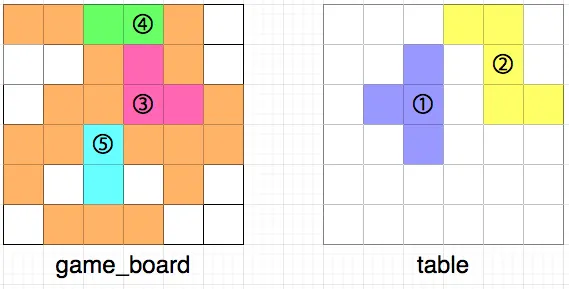
이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.
•
3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
•
5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.
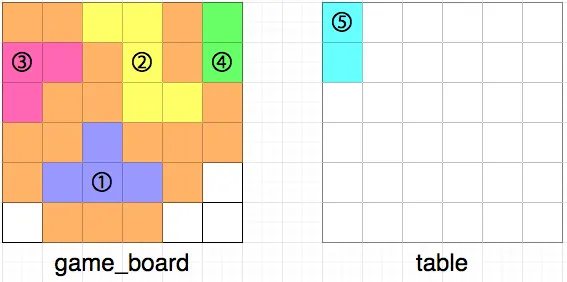
다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.
최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.
현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.
제한사항
•
3 ≤ game_board의 행 길이 ≤ 50
•
game_board의 각 열 길이 = game_board의 행 길이
◦
즉, 게임 보드는 정사각 격자 모양입니다.
◦
game_board의 모든 원소는 0 또는 1입니다.
◦
0은 빈칸, 1은 이미 채워진 칸을 나타냅니다.
◦
퍼즐 조각이 놓일 빈칸은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
•
table의 행 길이 = game_board의 행 길이
•
table의 각 열 길이 = table의 행 길이
◦
즉, 테이블은 game_board와 같은 크기의 정사각 격자 모양입니다.
◦
table의 모든 원소는 0 또는 1입니다.
◦
0은 빈칸, 1은 조각이 놓인 칸을 나타냅니다.
◦
퍼즐 조각은 1 x 1 크기 정사각형이 최소 1개에서 최대 6개까지 연결된 형태로만 주어집니다.
•
game_board에는 반드시 하나 이상의 빈칸이 있습니다.
•
table에는 반드시 하나 이상의 블록이 놓여 있습니다.
아이디어 및 해결 방법
코드
from collections import deque
class Block(object):
def __init__(self, pos):
rmin = min(p[0] for p in pos)
cmin = min(p[1] for p in pos)
pos = [(r-rmin, c-cmin) for r, c in pos]
self.pos = pos
self.R = max(p[0] for p in pos) + 1
self.C = max(p[1] for p in pos) + 1
self.mats = [
[[0] * self.C for _ in range(self.R)],
[[0] * self.R for _ in range(self.C)],
[[0] * self.C for _ in range(self.R)],
[[0] * self.R for _ in range(self.C)],
]
for r, c in pos:
self.mats[0][r][c] = 1
self.mats[1][c][self.R-1 - r] = 1
self.mats[2][self.R-1 - r][self.C-1 - c] = 1
self.mats[3][self.C-1 - c][r] = 1
def size(self):
return len(self.pos)
def __eq__(self, b):
return any(b == mat for mat in self.mats)
def bfs(board, r, c, vis):
R, C = len(board), len(board[0])
val = board[r][c]
q = deque()
q.append( (r, c) )
vis.add( (r, c) )
positions = []
while q:
r, c = q.popleft()
positions.append( (r, c) )
for dr, dc in [(0, 1), (0, -1), (1, 0), (-1, 0)]:
if (r+dr, c+dc) in vis:
continue
if 0 <= r+dr < R and 0 <= c+dc < C and board[r+dr][c+dc] == val:
q.append( (r+dr, c+dc) )
vis.add( (r+dr, c+dc) )
return positions
def solution(game_board, table):
R, C = len(table), len(table[0])
blanks = []
vis = set()
for r in range(R):
for c in range(C):
if game_board[r][c] == 0 and (r, c) not in vis:
positions = bfs(game_board, r, c, vis)
blanks.append( Block(positions) )
blocks = []
vis = set()
for r in range(R):
for c in range(C):
if table[r][c] == 1 and (r, c) not in vis:
positions = bfs(table, r, c, vis)
blocks.append( Block(positions) )
answer = 0
for b in blocks:
idx = -1
for i, blank in enumerate(blanks):
if b == blank:
idx = i
if idx != -1:
answer += b.size()
blanks.pop(idx)
return answer
Python
복사
출처
프로그래머스 코딩테스트 연습 https://school.programmers.co.kr/learn/challenges