문제 설명 및 제한사항
문제 설명
신규 게임 ‘카카오 미로 탈출’이 출시되어, 라이언이 베타테스터로 참가했습니다.
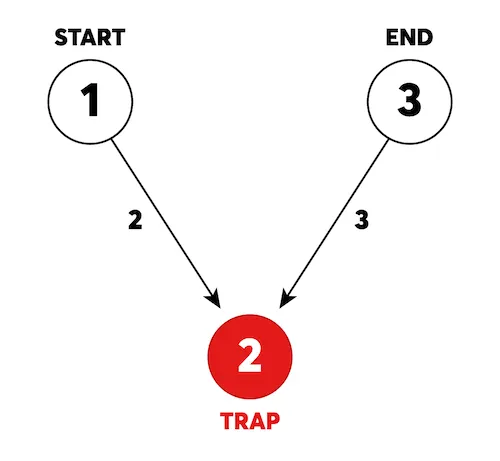
위 예시 그림은 카카오 미로 탈출의 초기 상태를 나타냅니다. 1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는데 걸리는 시간이 표시되어 있습니다. 길은 화살표가 가리키는 방향으로만 이동할 수 있습니다. 미로에는 함정이 존재하며, 함정으로 이동하면, 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.출발지점인 1번 방에서 탈출이 가능한 3번 방까지 이동해야 합니다. 탈출하는데 걸리는 최소 시간을 구하려고 합니다.
•
그림의 원은 방을 나타내며 원 안의 숫자는 방 번호를 나타냅니다.
◦
방이 n개일 때, 방 번호는 1부터 n까지 사용됩니다.
•
화살표에 표시된 숫자는 방과 방 사이를 이동할 때 걸리는 시간을 나타냅니다.
◦
화살표가 가리키고 있는 방향으로만 이동이 가능합니다. 즉, 위 그림에서 2번 방에서 1번 방으로는 이동할 수 없습니다.
•
그림에 표시된 빨간색 방인 2번 방은 함정입니다.
◦
함정 방으로 이동하는 순간, 이동한 함정 방과 연결되어있는 모든 길의 방향이 반대가 됩니다.
◦
위 그림 1번 방에서 2번 방으로 이동하는 순간 1에서 2로 이동할 수 있던 길은 2에서 1로 이동할 수 있는 길로 바뀌고, 3에서 2로 이동할 수 있던 길은 2에서 3으로 이동할 수 있는 길로 바뀝니다.
◦
똑같은 함정 방을 두 번째 방문하게 되면 원래 방향의 길로 돌아옵니다. 즉, 여러 번 방문하여 계속 길의 방향을 반대로 뒤집을 수 있습니다.
•
미로를 탈출하는데 필요한 최단 시간은 다음과 같습니다.
◦
1→2: 2번 방으로 이동합니다. 이동 시간은 2입니다.
◦
함정 발동: 2번 방과 연결된 모든 길의 방향이 반대가 됩니다.
◦
2→3: 3번 방으로 이동합니다. 이동 시간은 3입니다.
◦
탈출에 성공했습니다. 총 이동시간은 5입니다.
방의 개수를 나타내는 정수 n, 출발 방의 번호 start, 도착 방의 번호 end, 통로와 이동시간을 나타내는 2차원 정수 배열 roads, 함정 방의 번호를 담은 정수 배열 traps이 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최단 시간을 return 하도록 solution 함수를 완성해주세요.
제한사항
•
2 ≤ n ≤ 1,000
•
1 ≤ start ≤ n
•
1 ≤ end ≤ n
•
1 ≤ roads의 행 길이 ≤ 3,000
•
roads의 행은 [P, Q, S]로 이루어져 있습니다.
◦
P에서 Q로 갈 수 있는 길이 있으며, 길을 따라 이동하는데 S만큼 시간이 걸립니다.
◦
1 ≤ P ≤ n
◦
1 ≤ Q ≤ n
◦
P ≠ Q
◦
1 ≤ S ≤ 3,000
◦
서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있습니다.
•
0 ≤ traps의 길이 ≤ 10
◦
1 ≤ traps의 원소 ≤ n
◦
시작 방과 도착 방은 함정이 아닙니다.
•
항상 미로를 탈출할 수 있는 경우만 주어집니다.
아이디어 및 해결 방법
다익스트라 알고리즘의 응용으로 해결 가능합니다. 코드를 예쁘게 짠 것 같지는 않지만… 아이디어를 쉽게 이해하기에는 좋다고 생각합니다.
우선 이 문제를 어렵게 만드는 것은 노드에 방문하면 그 노드가 ‘뒤집힌’ 상태가 되면서 연결된 간선들의 방향이 전부 반대가 되는 성질 때문입니다. 즉, 어떤 노드에 두 번째 방문했을 때, 주변 간선의 방향이 달라져있을 수 있어서 이전 방문과는 “다른 상태”의 노드일 수 있다는 겁니다. 같은 노드지만 다른 노드로 생각해야 한다는 거죠. 따라서 다익스트라를 그냥 노드 ID만 가지고 돌리면 문제를 틀리게 됩니다.
여기서 “노드의 상태”란 결국 (노드의 ID, 그 노드가 뒤집힌 상태인지, 그 노드의 이웃이 뒤집혔는지) 의 튜플로 유일하게 결정됩니다. 따라서 기존 다익스트라의 dist 배열을 “노드 상태 튜플”을 key로 가지는 딕셔너리로 대체하고, “노드 상태 공간”에서의 다익스트라 알고리즘을 수행하면 문제를 해결할 수 있게 됩니다.
end 노드의 여러 상태 중 가장 작은 cost를 가지는 상태에서의 cost를 답안으로 제출하면 됩니다.
코드
from heapq import heappush, heappop
from collections import defaultdict
from math import inf
def solution(n, start, end, roads, traps):
traps = set(traps)
# 아래와 같은 entry들로 Adjacency list를 구성합니다.
# (이웃 노드, cost, 뒤집혔을 때 유효한 edge인지 여부)
A = defaultdict(list)
for u, v, w in roads:
A[u].append( (v, w, False) )
A[v].append( (u, w, True) )
# 다익스트라를 시도해봅니다.
flipped = [False] * (n+1) # 함정 노드가 뒤집혔는지 나타내는 flag입니다.
q = [(0, start, flipped)]
# 어떤 노드의 상태는 (노드 번호, 그 노드가 뒤집혔는지, 그 노드의 이웃이 뒤집혔는지) 여부로
# 유일하게 결정됩니다.
start_state = ( start, False, tuple([False] * len(A[start])) )
dist = {}; dist[start_state] = 0
while q:
d, u, flipped = heappop(q)
u_state = ( u, flipped[u], tuple(flipped[v] for v, _, _ in A[u]) )
if d > dist.get(u_state, inf):
continue
for v, w, valid_when_flipped in A[u]:
# u-v edge가 뒤집혔는지 아닌지 판단합니다.
# 노드 u, v 둘다 안 뒤집혔거나, 둘다 뒤집혔다면 edge는 그대로입니다.
edge_flipped = flipped[u] ^ flipped[v]
# valid_when_flipped이 False이면,
# u, v 둘다 안 뒤집혔거나, 둘다 뒤집혔을 때만 유효한 edge입니다.
# valid_when_flipped이 True이면,
# u, v 둘 중 하나만 뒤집혔을 때만 유효한 edge입니다.
if (valid_when_flipped is False and not edge_flipped) or \
(valid_when_flipped is True and edge_flipped):
f = flipped[:]
if v in traps:
f[v] = not f[v]
v_state = ( v, f[v], tuple(flipped[x] for x, _, _ in A[v]) )
if d + w < dist.get(v_state, inf):
dist[v_state] = d + w
heappush( q, (d+w, v, f) )
candidates = [dist[k] for k in dist if k[0] == end]
return min(candidates)
Python
복사
출처
프로그래머스 코딩테스트 연습 https://school.programmers.co.kr/learn/challenges