•
AlphaFold를 비롯한 단백질 구조 예측 모델 구현에서 개별 아미노산 residue들은 강체(rigid body)로 가정하며, 3차원 공간 상에서의 rotation (R) 과 translation (t)으로 표현되는 Euclidean transformation을 예측함으로써 아미노산의 위치와 배향을 정하게 된다.
•
그러면 각 아미노산의 원자 사이의 결합 길이와 각도는 상수로 취급한다는 건데, 어떤 값으로 정하면 될까? → 밝혀진 Peptide bond의 ideal (typical) geometry를 사용한다!
•
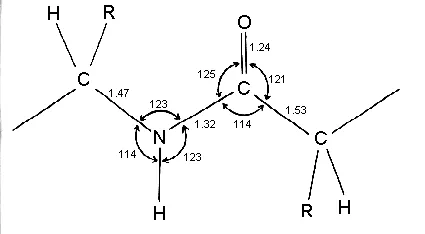
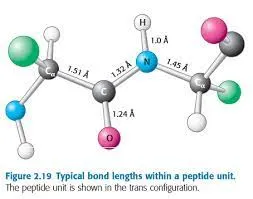
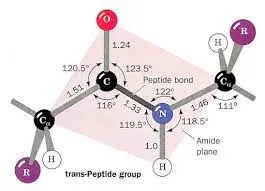
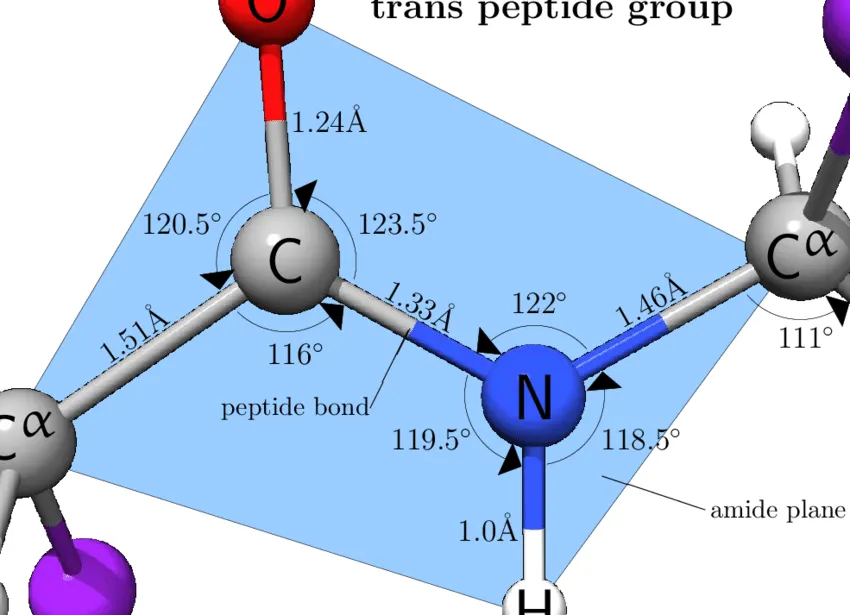
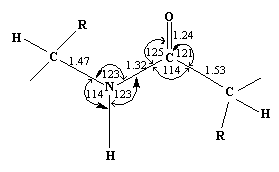
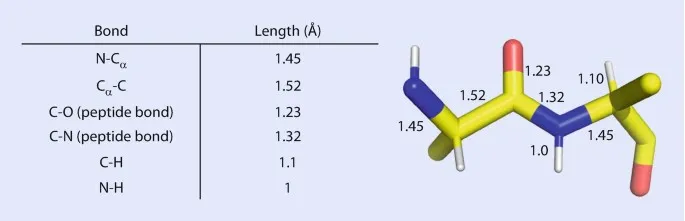
우선 여러 자료를 살펴보자.
•
위의 결과들을 취합해서 Ca, C, Cb, N 사이의 결합 길이와 결합각을 표로 정리해볼 수 있겠다.
결합각
결합 | 각도 (º) |
Ca - N - C | 122 ~ 123 |
Ca - C - N | 114 ~ 116 |
C - Ca - N | 111 |
결합길이
결합 | 길이 (A) |
Ca - C | 1.51 ~ 1.53 |
C - N | 1.32 ~ 1.33 |
N - Ca | 1.45 ~ 1.47 |
코드 예시
•
IgFold 에서는 residue 강체의 initialization을 다음과 같이 구현하고 있다. https://github.com/Graylab/IgFold/blob/main/igfold/utils/coordinates.py
def get_ideal_coords(center=False):
N = torch.tensor([[0, 0, -1.458]], dtype=float)
A = torch.tensor([[0, 0, 0]], dtype=float)
B = torch.tensor([[0, 1.426, 0.531]], dtype=float)
C = place_fourth_atom(
B,
A,
N,
torch.tensor(2.460), # length
torch.tensor(0.615), # planar
torch.tensor(-2.143), # dihedral
) # this produces tensor([[-1.1932, -0.7685, 0.551]])
coords = torch.cat([N, A, C, B]).float()
if center:
coords -= coords.mean(
dim=0,
keepdim=True,
)
return coords
def place_fourth_atom(
a_coord: torch.Tensor,
b_coord: torch.Tensor,
c_coord: torch.Tensor,
length: torch.Tensor,
planar: torch.Tensor,
dihedral: torch.Tensor,
) -> torch.Tensor:
"""
Given 3 coords + a length + a planar angle + a dihedral angle, compute a fourth coord
"""
bc_vec = b_coord - c_coord
bc_vec = bc_vec / bc_vec.norm(dim=-1, keepdim=True)
n_vec = (b_coord - a_coord).expand(bc_vec.shape).cross(bc_vec)
n_vec = n_vec / n_vec.norm(dim=-1, keepdim=True)
m_vec = [bc_vec, n_vec.cross(bc_vec), n_vec]
d_vec = [
length * torch.cos(planar),
length * torch.sin(planar) * torch.cos(dihedral),
-length * torch.sin(planar) * torch.sin(dihedral)
]
d_coord = c_coord + sum([m * d for m, d in zip(m_vec, d_vec)])
return d_coord
Python
복사
•
우선 N, Ca, Cb 사이의 길이를 재 보면, N-Ca는 1.458, Ca-Cb 사이는 1.52165601 정도로 나타난다. Ca-Cb의 bond length는 자료에는 나와있지는 않지만, 직접 단백질 구조 데이터 받아서 확인해 봐도 1.52~1.53 근처로 나타난다.
•
참고로 C-N 사이의 거리는 2.447로 나타나는데, 제2코사인법칙을 써서 이론적인 결합각/결합길이로부터 C-N 거리 구해보면 아래와 같다. 대략적으로 2.44 정도로 같다.
•
그러면 이제 place_fourth_atom을 이해해보자. Ca, Cb, N의 위치가 주어졌을 때 C의 위치를 특정하는 함수일 텐데, 어떻게 계산해내는지 보자. 구하고자 하는 점을 X라고 할 때, 파라미터를 설명하면
◦
a_coord, b_coord, c_coord 가 주어진다.
◦
length는 c_coord에서 새로 계산할 원자의 위치 까지의 거리이다.
◦
planar는 XCB의 각도
◦
dihedral은 XCB가 이루는 평면과, ACB가 이루는 평면의 이면각
•
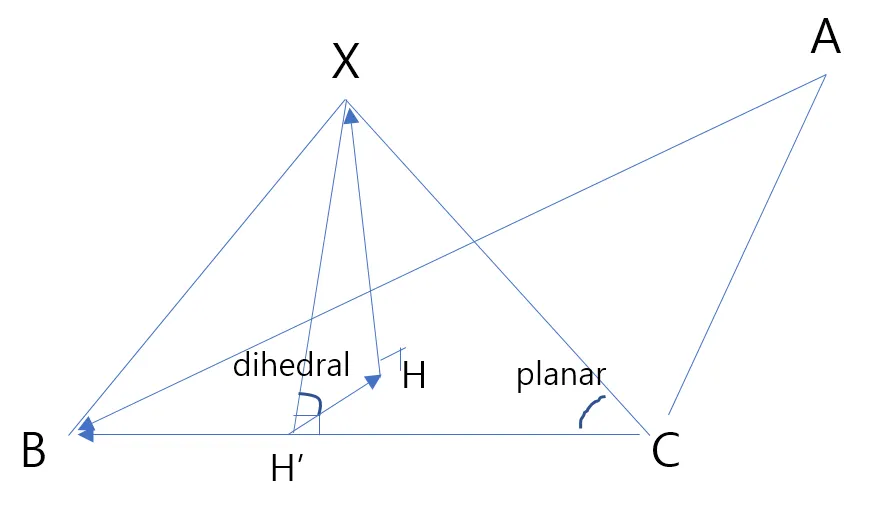
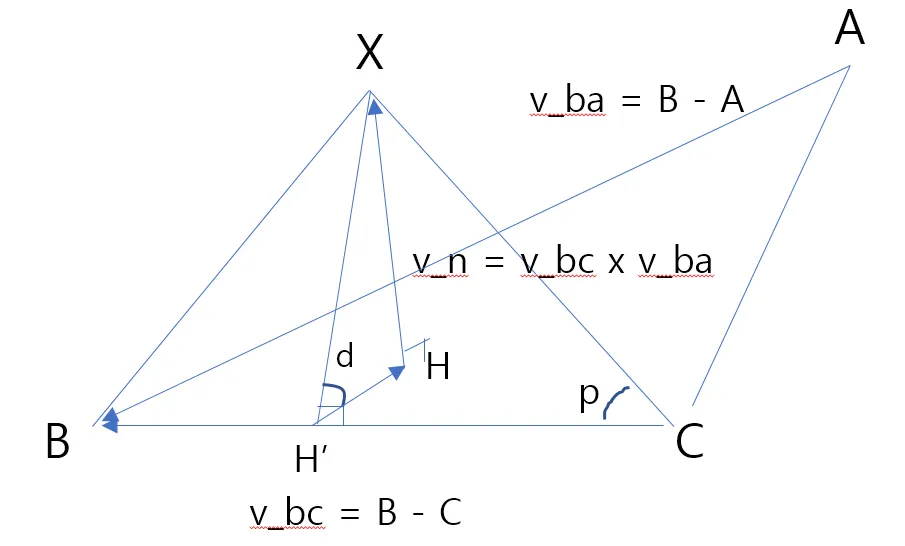
그림으로 표현하면 아래와 같다.
•
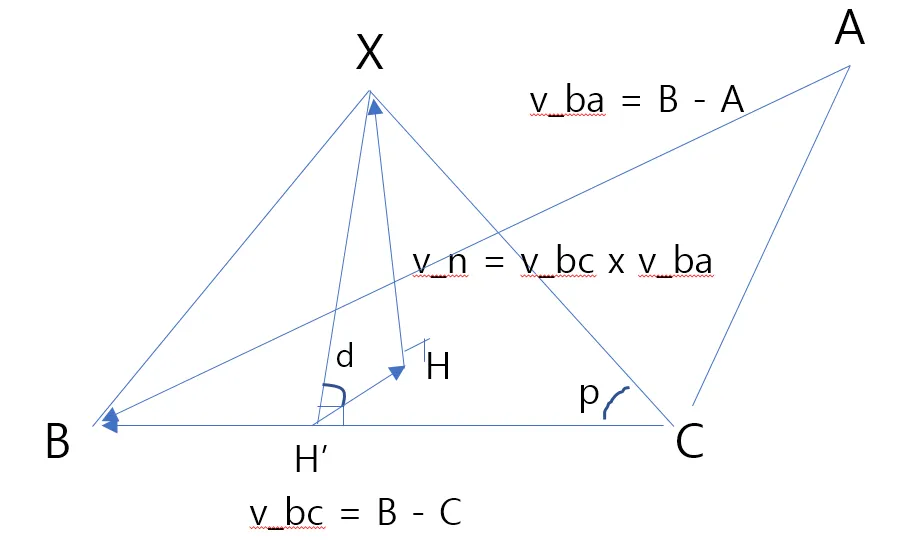
결국 위 그림에서 벡터 CX만 잘 구하면 되는 것이다! 열심히 배웠던 기하와 벡터를 잘 떠올려보자…
•
먼저 X에서 평면 ABC에 내린 수선의 발을 H라 하면 평면 ABC의 법선벡터 HX는 벡터 CB와 AB의 외적이다. 위 함수에서는 단위벡터로 normalize 해주고 있다. 외적 할때는 순서에 주의해야 함을 잊지 말자. 오른손 법칙으로 방향이 정해지니까.
◦
참고로 IgFold 구현에서는 AB x CB 한 다음 벡터에 (-1)을 곱해서 방향을 뒤집어 준다.
•
그 다음, H에서 선분 BC에 내린 수선의 발을 H’라 하면 벡터 H’H는 벡터 CB와 벡터 HX (v_n)의 외적이다.
◦
참고로 IgFold 구현에서는 v_n이 이미 방향이 반대이므로, 벡터 HX와 벡터 CB의 외적을 해준다.
•
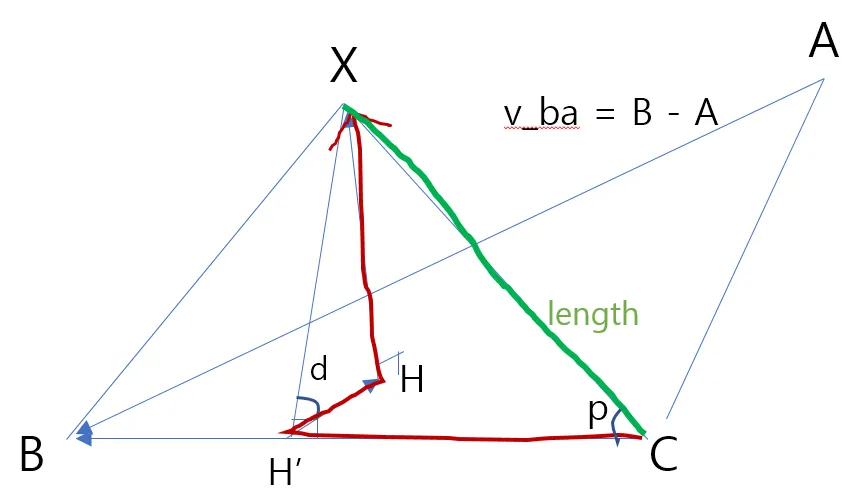
이제 CX 벡터 구하기는 사실상 끝났다. 벡터 CH’ + H’H + HX를 하면 된다.
◦
CH’는 CB 단위벡터 * (XC의 길이 * cos(p))
◦
H’H는 H’H 단위벡터 * (XC의 길이 * sin(p) * cos(d))
◦
HX는 HX 단위벡터 * (XC의 길이 * sin(p) * sin(d))
•
그래서 코드로 나타내면 아래와 같이 되는 것
d_vec = [
length * torch.cos(planar) * bc_vec,
length * torch.sin(planar) * torch.cos(dihedral) * n_vec.cross(bc_vec),
-length * torch.sin(planar) * torch.sin(dihedral) * n_vec
]
Python
복사
•
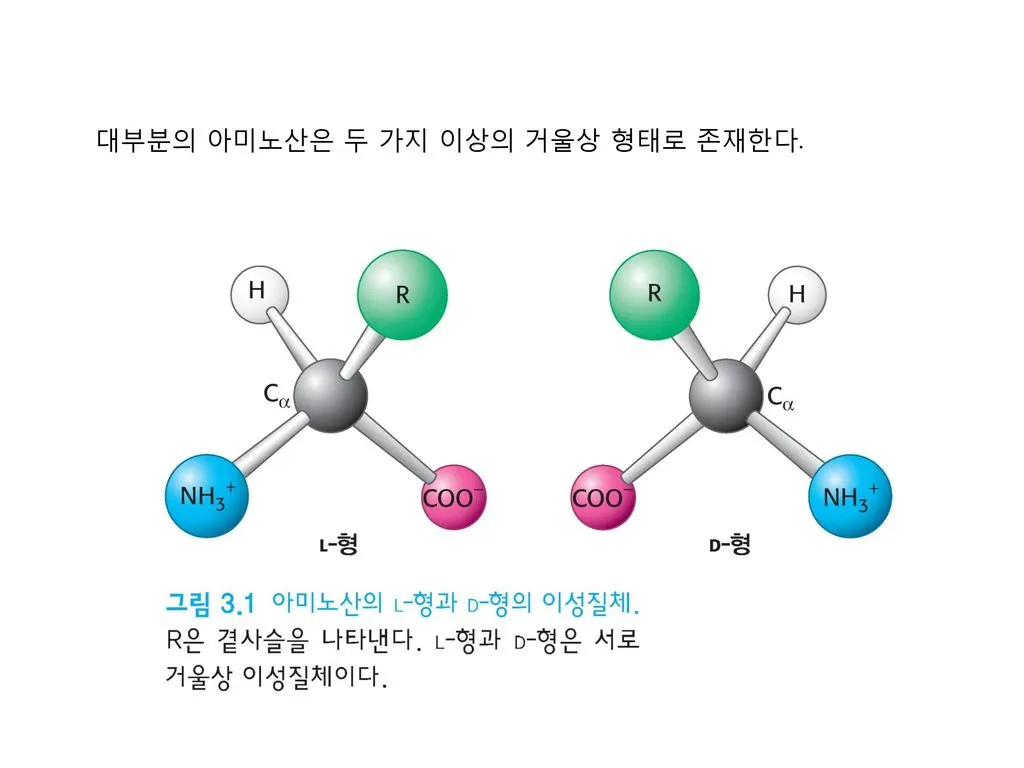
파라미터를 넘겨줄 때, 입체이성질체 잘 고려해서 넘겨줘야겠다.