Over-confidence problem
•
Input distribution이 training data와 약간 달라지면, neural network들이 매우 높은 confidence로 틀린 예측값을 제공함.
◦
Adversarial example에 취약 → 사람 눈으로 구별되지 않는 차이, 그러나 전혀 다른 prediction
왜 over-confident한가?
1.
Decision boundary가 sharp하고 data에 가깝기 때문
2.
대부분의 hidden representation space에 높은 confidence의 prediction 값이 할당되어 있음.
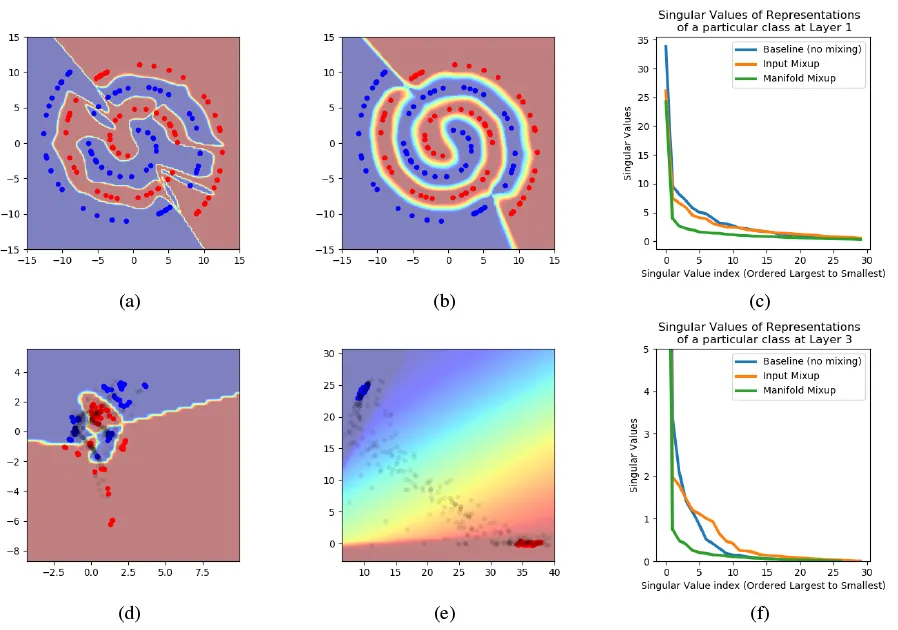
Manifold mixup의 효과
(a) Vanilla training 시의 decision boundary. (b) Manifold mixup 사용 시의 decision boundary. 더 smooth하다. (c) Layer 1의 representation들의 singular values. Manifold mixup representation들이 더 적은 representation으로 더 큰 데이터 variance를 설명하고 있다. (d) Vanilla training 시의 hidden representation. (e) Manifold mixup 사용 시의 hidden representation. (f) → (c)와 마찬가지.
Manifold mixup improves the hidden representations and decision boundaries of neural networks at multiple layers.
Manifold mixup
•
Deep neural network 를 학습한다고 하자.
•
Manifold mixup은 5단계로 수행된다:
1.
Network 내의 eligible layer의 집합 로부터 random layer 를 선정한다.
a.
Input layer도 포함될 수 있다 → 이 경우는 input mixup과 동일
2.
두 개의 minibatch 와 를 layer 까지 forward-propagate한다.
a.
결과로 와 를 얻는다.
3.
이 minibatch에 input mixup을 적용한다.
a.
결과로 “mixed minibatch” 를 얻는다.
이 때, 이고,
4.
이후는 input mixup처럼 진행. 생략